Danger_RSA
题目
1 | from Crypto.Util.number import * |
题解
e的位数为34位,也就是s和t的位数大约都为17位左右,可以推出来a的值为4
求出所有的s和t的可能值,然后判断是否满足,最终找到s和t的值
t=91903,s=120561
1 | s = 120561 |
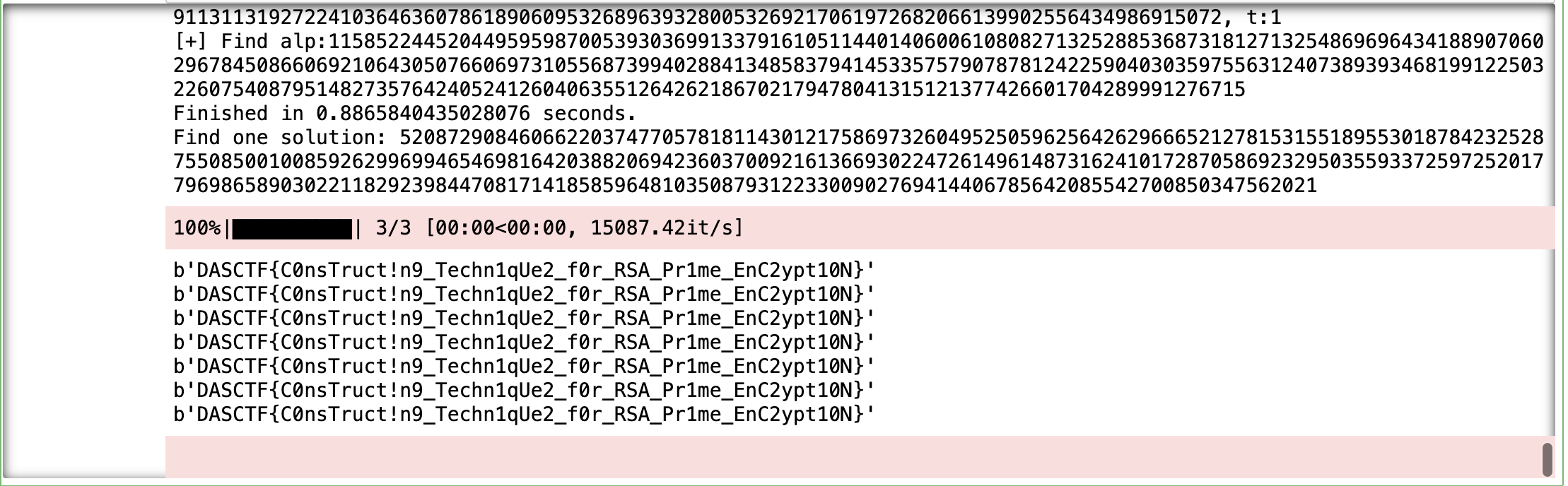
求出p和q的值之后,就是属于e和phi不互素的情况,而且此时的e比较大,可以考虑AMM算法求解
1 | import random |
Easy_3L
题目
1 | from gmpy2 import * |
题解
两个加密函数和一个密钥生成函数,但是p和h的值已经给了,密钥生成函数可以不用考虑了
明文是通过encrypt1加密的主要是个LCG的加密过程
s[3]是通过encrypt2加密,通过encrypt2可以还原s[3],带入encrypt1中再求m
1 | p = 25886434964719448194352673440525701654705794467884891063997131230558866479588298264578120588832128279435501897537203249743883076992668855905005985050222145380285378634993563571078034923112985724204131887907198503097115380966366598622251191576354831935118147880783949022370177789175320661630501595157946150891275992785113199863734714343650596491139321990230671901990010723398037081693145723605154355325074739107535905777351 |
求出S3之后,就是对LCG算法的逆过程
此处的LCG属于a,b,n都未知的情况
参考链接:LCG_CTF
1 | from Crypto.Util.number import * |

easyRSA
题目
1 | from gmpy2 import invert |
题解
给了n和d,要分解n
先求e
1 | n = 80642592772746398646558097588687958541171131704233319344980232942965050635113860017117519166348100569115174644678997805783380130114530824798808098237628247236574959152847903491509751809336988273823686988619679739640305091291330211169194377552925908412183162787327977125388852329089751737463948165202565859373 |
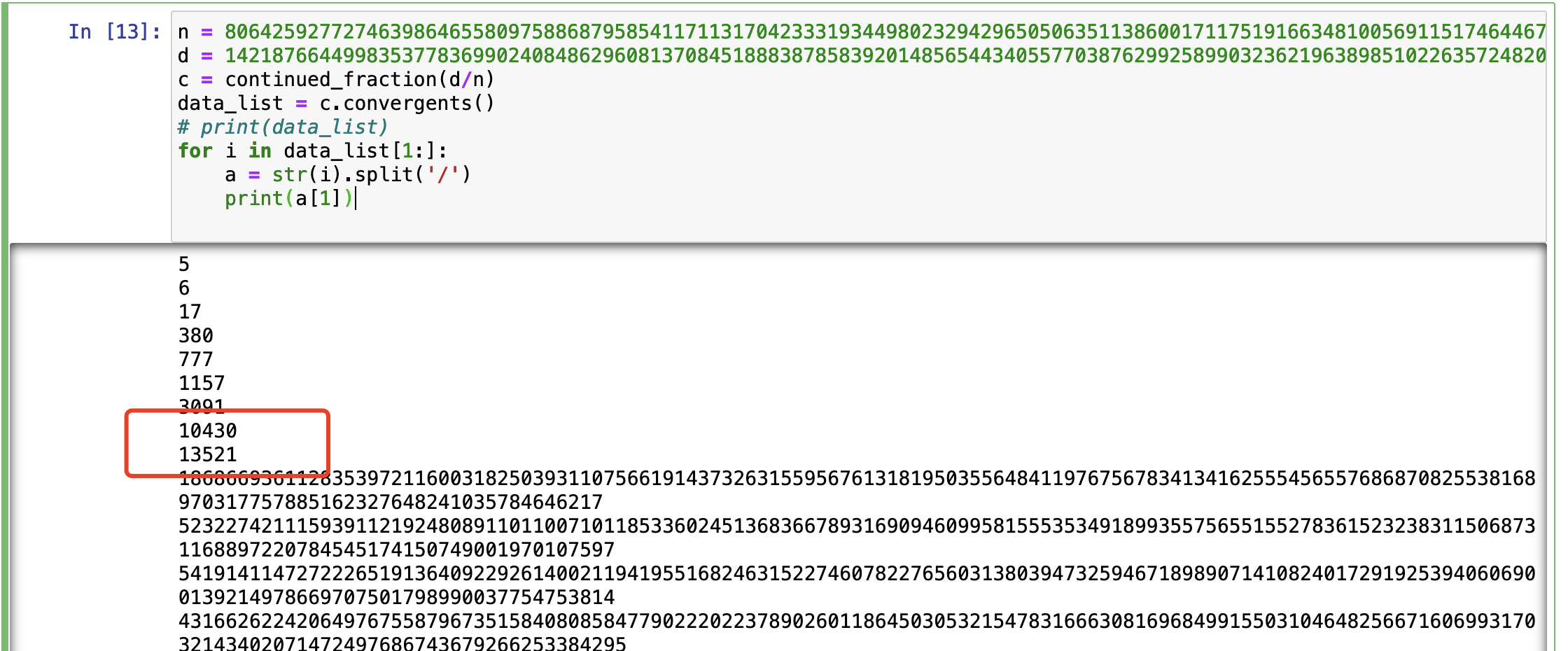
通过判断e=13521
有了e,d,n就可以分解n了
1 | from math import gcd |

XOR贯穿始终
题目
1 | 自由和谐和谐富强公正友善爱国公正法治法治文明和谐自由法治自由法治平等公正友善公正公正民主法治自由公正敬业和谐富强公正友善爱国和谐平等平等友善敬业法治敬业和谐富强法治平等平等友善敬业公正公正公正友善敬业法治平等平等诚信自由公正自由平等友善敬业公正友善法治和谐和谐 |
1 | from gmpy2 import gcd |
1 | -----BEGIN PRIVATE KEY----- |
题解
先核心价值观解码
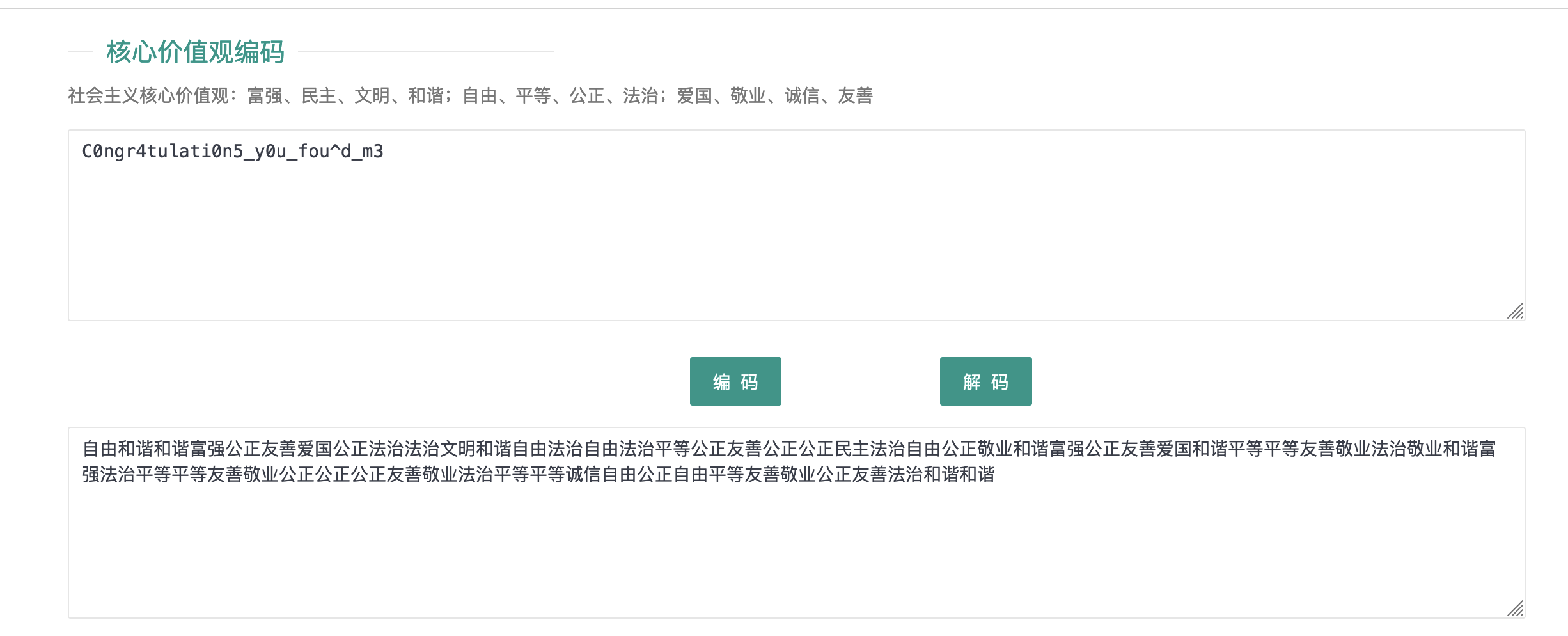
剩下的就是私钥文件格式解析
参考链接:http://tttang.com/archive/1670/
参考链接:https://zhuanlan.zhihu.com/p/461349946

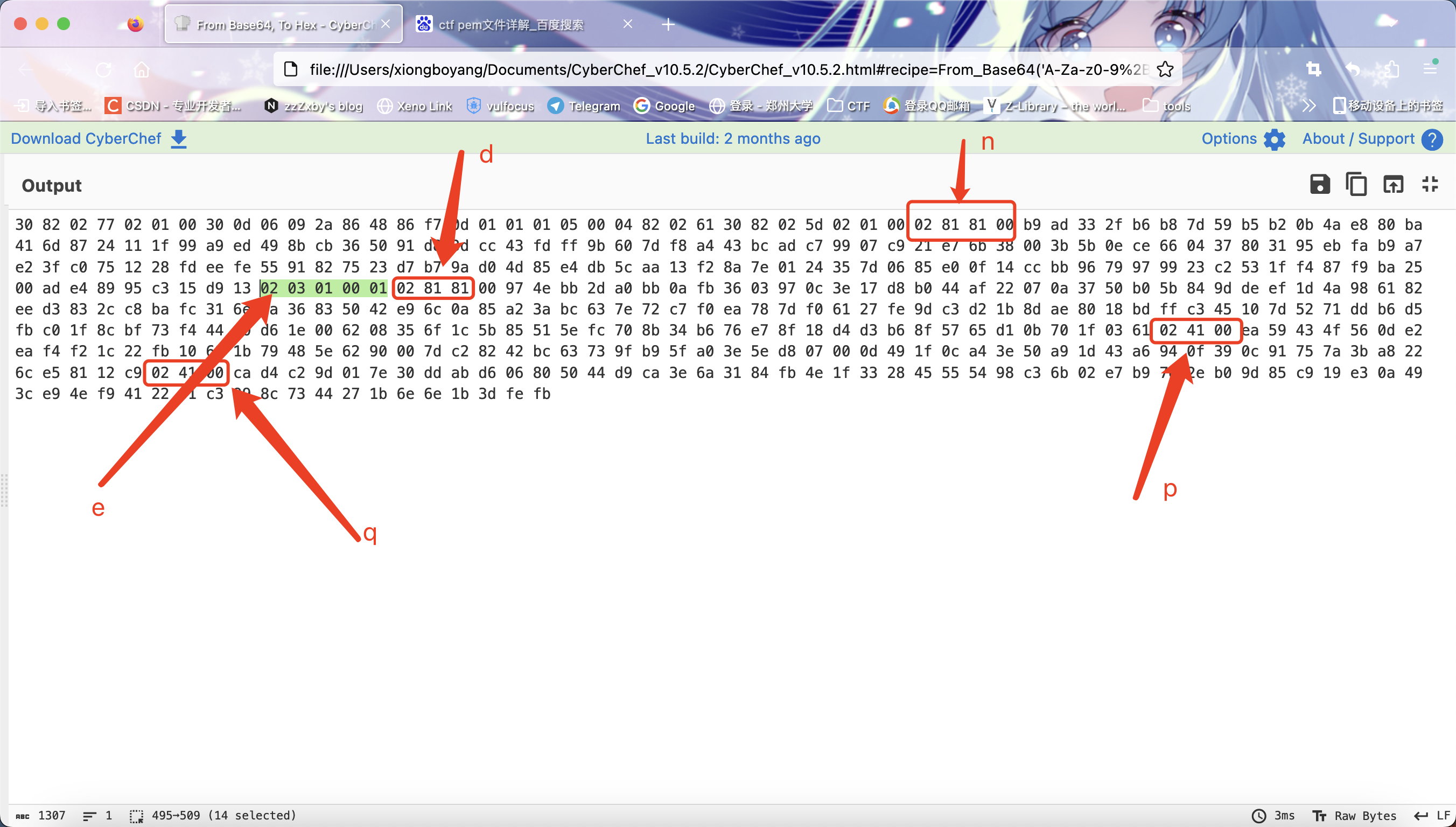
有了私钥,直接解密
结果还需要跟上述的字符串异或,得到正确flag
1 | from Crypto.Util.number import * |

MCeorpkpleer
题目
1 | from Crypto.Util.number import * |
题解
加密代码主要是RSA,其中p泄漏了高位可以通过coppersmith恢复
剩下的就是e没有给出,e为64位,根据已知的信息可以看出e是通过背包密码得到en_e的
先恢复p
1 | from Crypto.Util.number import * |
list列表的第一个数是1,那么pubkey列表的第一个元素就是w
有了w就可以求m了
1 | from Crypto.Util.number import * |
剩下的就是通过背包密码还原e
解决背包问题简单的方法就是利用格
构造如下的格
1 | pubkey = [18143710780782459577, 54431132342347378731, 163293397027042136193, 489880191081126408579, 1469640573243379225737, 4408921719730137677211, 13226765159190413031633, 39680295477571239094899, 119040886432713717284697, 357122659298141151854091, 1071367977894423455562273, 3214103933683270366686819, 9642311801049811100060457, 28926935403149433300181371, 86780806209448299900544113, 260342418628344899701632339, 781027255885034699104897017, 2343081767655104097314691051, 7029245302965312291944073153, 21087735908895936875832219459, 63263207726687810627496658377, 189789623180063431882489975131, 569368869540190295647469925393, 1708106608620570886942409776179, 601827224419797931380408071500, 1805481673259393794141224214500, 893952418336266652976851386463, 2681857255008799958930554159389, 3523079163584485147344841221130, 1524252287869625983140881149316, 50264262166963219975822190911, 150792786500889659927466572733, 452378359502668979782399718199, 1357135078508006939347199154597, 4071405235524020818041597463791, 3169230503688232995231149877299, 462706308180869526799807117823, 1388118924542608580399421353469, 4164356773627825741198264060407, 3448085117999647764701149667147, 1299270151115113835209806487367, 3897810453345341505629419462101, 2648446157152195057994615872229, 3422845870014670444537026359650, 1223552407160181874717436564876, 3670657221480545624152309694628, 1966986461557807413563286569810, 1378466783231507511243038452393, 4135400349694522533729115357179, 3361215846199738142293703557463, 1038662335715384967987468158315, 3115987007146154903962404474945, 302975818554635252993570910761, 908927455663905758980712732283, 2726782366991717276942138196849, 3657854499533237101379593333510, 1928578295715881845245137486456, 1263242285705730806288591202331, 3789726857117192418865773606993, 2324195368467747797703678306905, 2450093503961328663664213663678, 2827787910442071261545819733997, 3960871129884299055190637944954, 2837628186769067706678271320788] |
最短向量不在第一行,打印结果,找到可能的目标向量
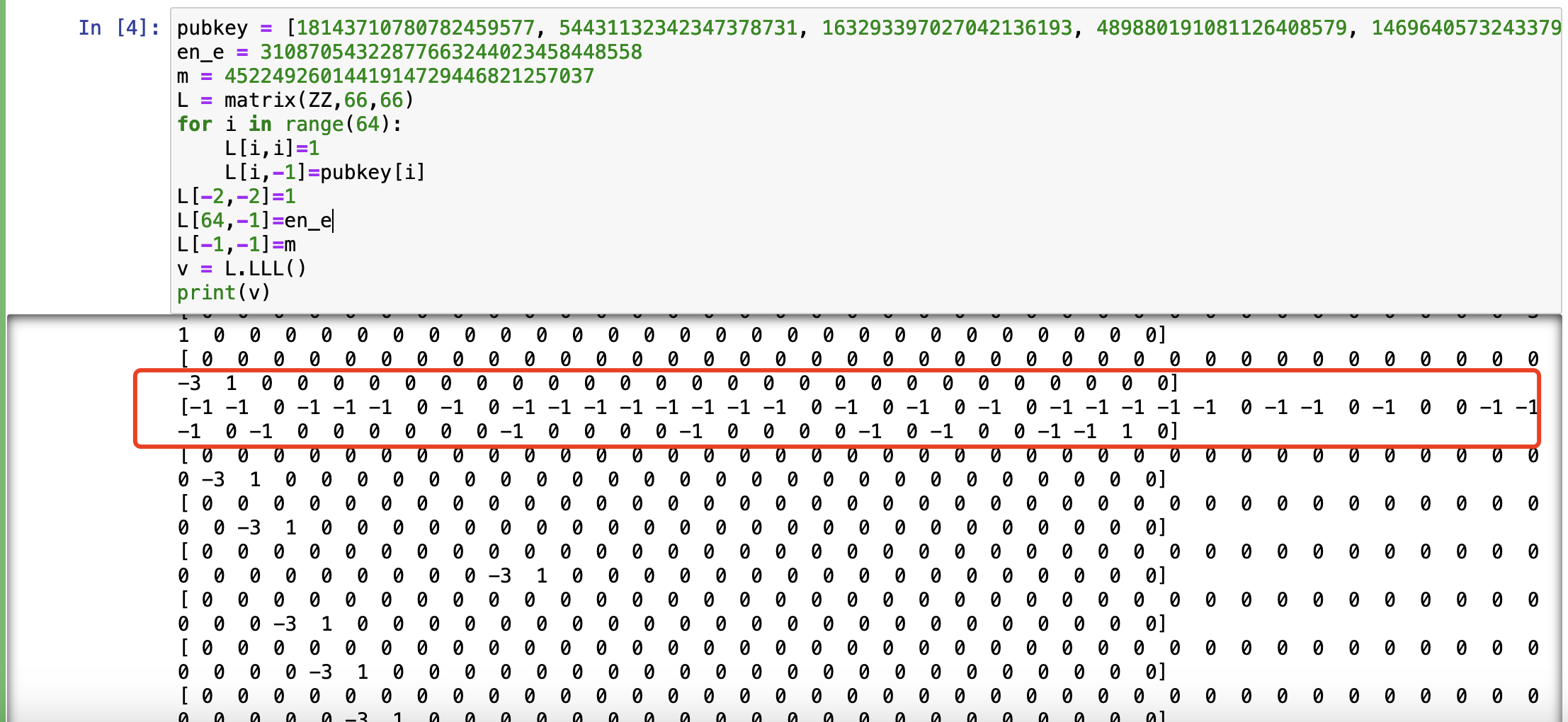
求出e后,就可以正常求解RSA
1 | from Crypto.Util.number import * |

signinCrypto
题目
1 | from random import * |
题解
flag的加密过程主要就是采用一个DES的CBC加密模式进行的,纵观代码,这道题的求解关键也就是求DES加密过程的KEY和IV
先求K1
DES加密采用64位密钥,实际上只用了56位,K2和K3都是64位,K1应该也为64位
这样一来,K1和hint异或的结果会泄漏hint的数据,从而求出hint,进而求出K1
1 | from Crypto.Util.number import * |
K3为flag的前八个字节,flag的格式为DASCTF{***},这里已经泄漏了七位,最后一位可以通过爆破求出
K2利用的是随机数预测
分析一下下面的代码
1 | def Rand(): |
List1里存的是624个16位的随机数,List2里存的是312个64位的随机数
task.txt中写的数据,前624为List1的数据
1 | file.write(hex((rand64 & 0xffff) | ((rand64 >> 32) & 0xffff) << 16) + "\\n") |
对每个随机数进行位操作,提取低 16 位和次高 16 位,并将它们合并为一个 32 位的整数,然后转换为十六进制,并将其写入文件,每个随机数占一行。
这里MT19937生成32位的随机数,对于16位的随机数,是先产生一个32位的随机数,然后取高16位输出
对于64位的随机数,则是生成两个32位的随机数,将第二个数做高位第一个数做低位输出
代码中初始化过seed,List1中存的就是624个32位随机数的高16位,List2经过处理后输出到文本中的数据泄漏了低16位,至此,可以获得624个32位的随机数,从而预测下一个随机数也就是K2
1 | from randcrack import RandCrack |
K1,K2,K3都解决了,剩下的就是求解IV
DES加密采用CBC模式,IV一般是64位
1 | hint2=(bytes_to_long(IV)<<32)^bytes_to_long(os.urandom(8)) |
IV左移32位,使得高32位没有受到影响,也就是说IV1可以通过hint2转字节直接获得
IV1为GWHT,然后求IV2
打印digest然后分段,发现前半部分和后半部分一致,说明IV1=IV2
1 | from Crypto.Util.number import * |
至此,就剩爆破K3,解密DES了
1 | from Crypto.Cipher import DES3 |
